Please Excuse My Dear Aunt Sally, she downloaded a shitty ad-infested calculator from the Google Play store.
Unfortunately, it’s the best calculator I could find so far (for my own needs). I paid to remove the ads though, ads bother me way too much to use something infested with them.
If you’re willing to pirate (or legally generate) a TI calculator ROM, then Graph 89 is probably what you’re looking for. This is what I use as my daily driver calculator with a TI-89 ROM.

Graph 89 with my TI-84 Plus Silver yields the bad answer
wabbitemu!!! Its literally a ti emulator
I’m with the right answer here. / and * have same precedence and if you wanted to treat
2(2+2)as a single unit, you should have written it like(2*(2+2)).It’s pretty common even in academic literature to treat implied multiplication as having higher precedence than explicit multiplication/division. Otherwise an expression like 1 / 2n would have to be interpreted as (1 / 2) * n rather than the more natural 1 / (2 * n).
A lot of this bullshit can be avoided with better notation systems, but calculators tend to be limited in what you can write, so meh. Unless you want to mislead people for the memes, just put parentheses around things.
That’s fair. Personally, I just have a grudge against math notation in general. Makes my programmer brain hurt when there’s no consistency and a lot of implicit rules.
Then again, I also like Lisp so I’m not exactly without sin.
As a musician, can I just say: I would give my right nut for a musical notation system that is as clearly defined as mathematical notation. The worst part is that everyone that attempts to fix musical notation, just creates a new standard of notation.
I know what video you linked even without clicking lol. Yeah, I can agree there. Although my only experience with music was “try to learn guitar, get distracted because ADHD”.
The rocksmith game might help you.
Even guitarhero/rockband will help you with using your fingers and will help when you want to try a real guitar. Muscle memory might not be great but for someone who is just doing it for fun it will be helpful getting your fretting and strumming coordination. And them being games might help fend off the adhd enough to keep you motivated to pick it up again after putting it down
I appreciate the sentiment, but I really don’t have time for another hobby.
I did accidentally become a DM for not one but two DnD groups recently.
I started with piano, technically, but I was 3-4 years old, and don’t remember any of it. I can sit a piano and make it sound good, but I can’t play sheet music on it. I switched to violin in second grade, and then just learned how to play everything except for rhythm guitar, and piano. Chords mess with my fingers. Strangely enough my ADHD allowed me to super focus, but I never got the hang of sight reading, so I mostly play by ear, but no one can tell.
I can even play a didgeridoo, and that required me to learn circular breathing.
That’s impressive!
My ADHD just makes me lose time. Blink and the day is just gone.
The problem is whether or not that rule is taught depends on when and where you learned it. Schools only started teaching that rule relatively recently, and even then, not universally. Which of course makes for ideal engagement bait on your hellsite of choice.
watches the people with basic math skills fight to the death over the answer
If you really wanna see a bloodbath, watch this:
You know that a couple has two children. You go to the couple’s house and one of their children, a young boy, opens the door. What is the probability that the couple’s other child is a girl?
This is basically Monty Hall right? The other child is a girl with 2/3 probability, because the first one being a boy eliminates the case where both children are girls, leaving three total cases, in two of which the other child is a girl (BG, GB, BB).
Cheeky bastard.
It is 50-50, though. The remaining possible states are BG and BB. Both are equally likely. Any further inference is narrative… not statistics.
The classic example of this is flipping 100 coins. If you get heads 99 times in a row… the last coin is still 50-50. Yes, it is obscenely unlikely to get heads 100 times in a row. But it’s already obscenely unlikely to get heads 99 times in a row. And it is obscenely unlikely to alternate perfectly between heads and tails. And it is obscenely unlikely to get a binary pattern spelling out the alphabet. And it is obscenely unlikely to get… literally any pattern.
Every pattern is equally unlikely, with a fair coin. We see 99 heads in a row versus 1 tails at the end, and think it narrowly averted the least-probable outcome. But only because we lump together all sequences with exactly one tails. That’s one hundred different patterns. 1-99 is not the same as 99-1. We just treat them the same because we fixate on uniformity.
Compare a non-binary choice: a ten-sided die. Thirty 1s in a row is about as unlikely as 100 heads in a row. But 1 1 1… 2 is the same as 1 1 1… 3. Getting the first 29 is pretty damn unlikely. One chance in a hundred million trillion. But the final die can land on any number 1-10. Nine of them upset the pattern our ape brains want. Wanting it doesn’t make it any more likely. Or any less likely.
It would be identically unlikely for a 10-sided die to count from 1 to 10, three times in a row. All the faces appear equally. But swap any two events and suddenly it doesn’t count. No pun intended.
If this couple had eight children, for some god-forsaken reason, and you saw seven boys, the eighth kid being another boy is not less likely for it. The possibility space has already been reduced to two possibilities out of… well nine, I suppose, if order doesn’t matter. They could have 0-8 boys. They have at least 7. The only field that says the last kid’s not a coin toss is genetics, and they say this guy’s chromosome game is strong.
You’re right, but it’s not a subversion of the Gambler’s Fallacy, it’s a subversion of conditional probability. A classic example is that I have two kids, and at least one of them is a boy. What is the probability that I have two boys?
The intuitive answer is 50%, because one kid’s sex doesn’t affect the other. But when I told you that I have two kids, there were four possibilities: GG, GB, BG, or BB. When I told you that at least one of them is a boy, all I did was take away the GG option. That means there’s only a 1 in 3 chance that I have two boys.
But by having one child answer the door, I change it yet again–now we know the sex of a particular child. We know that the child who opened the door is a boy. This is now akin to saying “I have two children, and the eldest is a boy. What is the possibility that I have two boys?” It’s a sneaky nerd snipe, because it targets specifically people who know enough about statistics to know what conditional probability is. It’s also a dangerous nerd snipe, because it’s entirely possible that my reasoning is wrong!
Different compilers have robbed me of all trust in order-of-operations. If there’s any possibility of ambiguity - it’s going in parentheses. If something’s fucky and I can’t tell where, well, better parenthesize my equations, just in case.
This is best practice since there is no standard order of operations across languages. It’s an easy place for bugs to sneak in, and it takes a non-insignificant amount of time to debug.
This is why I loved my Casio 2D. It could use actual fractions to avoid these kind of issues
In some countries we’re taught to treat implicit multiplications as a block, as if it was surrounded by parenthesis. Not sure what exactly this convention is called, but afaic this shit was never ambiguous here. It is a convention thing, there is no right or wrong as the convention needs to be given first. It is like arguing the spelling of color vs colour.
This is exactly right. It’s not a law of maths in the way that 1+1=2 is a law. It’s a convention of notation.
The vast majority of the time, mathematicians use implicit multiplication (aka multiplication indicated by juxtaposition) at a higher priority than division. This makes sense when you consider something like 1/2x. It’s an extremely common thing to want to write, and it would be a pain in the arse to have to write brackets there every single time. So 1/2x is universally interpreted as 1/(2x), and not (1/2)x, which would be x/2.
The same logic is what’s used here when people arrive at an answer of 1.
If you were to survey a bunch of mathematicians—and I mean people doing academic research in maths, not primary school teachers—you would find the vast majority of them would get to 1. However, you would first have to give a way to do that survey such that they don’t realise the reason they’re being surveyed, because if they realise it’s over a question like this they’ll probably end up saying “it’s deliberately ambiguous in an attempt to start arguments”.
The real answer is that anyone who deals with math a lot would never write it this way, but use fractions instead
BDMAS bracket - divide - multiply - add - subtract
BEDMAS: Bracket - Exponent - Divide - Multiply - Add - Subtract
PEMDAS: Parenthesis - Exponent - Multiply - Divide - Add - Subtract
Firstly, don’t forget exponents come before multiply/divide. More importantly, neither defines wether implied multiplication is a multiply/divide operation or a bracketed operation.
16
deleted by creator
Ah damn it. It took me ages to find a calculator app that fits my needs… And now I find out it works like the one on the right.
… the one on the right is correct… that’s a jank ass calculator on the left that doesn’t know how to do order of operations 8/2×(2+2) 8/2x4 4x4 16
There isn’t a multiplication symbol though. By your logic something like
8÷2xwould mean(8÷2)*xbecause order of operationsOr if you read
8÷2√xas(8÷2)*√xJust notate
8÷2(2+2)as8÷2x; x=(2+2)and you get it, you can substitute any complete expression with a variable in an equation and the logic stays the same.You know sometimes both are correct.
deleted by creator
The problem is that there’s no “external” parentheses to really tell us which is right:
(8 / 2) * 4or8 / (2 * 4)The amount of comments here shows how much debate this “simple” thing generates
[…] the question is ambiguous. There is no right or wrong if there are different conflicting rules. The only ones who claim that there is one rule are the ones which are wrong!
https://people.math.harvard.edu/~knill/pedagogy/ambiguity/index.html
As youngsters, math students are drilled in a particular
convention for the “order of operations,” which dictates the order thus:
parentheses, exponents, multiplication and division (to be treated
on equal footing, with ties broken by working from left to right), and
addition and subtraction (likewise of equal priority, with ties similarly
broken). Strict adherence to this elementary PEMDAS convention, I argued,
leads to only one answer: 16.Nonetheless, many readers (including my editor), equally adherent to what
they regarded as the standard order of operations, strenuously insisted
the right answer was 1. What was going on? After reading through the
many comments on the article, I realized most of these respondents were
using a different (and more sophisticated) convention than the elementary
PEMDAS convention I had described in the article.In this more sophisticated convention, which is often used in
algebra, implicit multiplication is given higher priority than explicit
multiplication or explicit division, in which those operations are written
explicitly with symbols like x * / or ÷. Under this more sophisticated
convention, the implicit multiplication in 2(2 + 2) is given higher
priority than the explicit division in 8÷2(2 + 2). In other words,
2(2+2) should be evaluated first. Doing so yields 8÷2(2 + 2) = 8÷8 = 1.
By the same rule, many commenters argued that the expression 8 ÷ 2(4)
was not synonymous with 8÷2x4, because the parentheses demanded immediate
resolution, thus giving 8÷8 = 1 again.This convention is very reasonable, and I agree that the answer is 1
if we adhere to it. But it is not universally adopted.Left is correct; implicit multiplication takes precedence over explicit multiplication or division.
What the fuck is the difference in implicit vs explicit? It’s the same operation, why the fuck does it matter if there is a symbol?
Multiplication comes first, then division.
Division is a form of Multiplication, just as subtraction is a form of addition. You multiply and divide in the same step, left to right
No, multiplication and division are resolved from left to right in the same step. But implicit multiplication (
xy, as opposed tox*y) happens first.
spoiler
For anyone like me who has math as their worst subject: PEMDAS.
PEMDAS is an acronym used to mention the order of operations to be followed while solving expressions having multiple operations. PEMDAS stands for P- Parentheses, E- Exponents, M- Multiplication, D- Division, A- Addition, and S- Subtraction.
So we gotta do it in the proper order. And remember, if the number is written like
2(3)then its multiplication, as if it was written2 x 3or2 * 3.So we read
8/2(2+2)and need to do the following;- Read the Parentheses of
(2 + 2)and follow the order of operations within them, which gets us 4. - Then we do
2(4)which is the same as2 x 4which is8 8 / 8is1.
The answer is 1. The old calculator is correct, the phone app which has ads backed into it for a thing that all computers were invented to do is inaccurate.
EDIT: Turns out I’m wrong, but I haven’t been told how or why. I’m willing to learn if people actually tell me, instead of call me wrong and keep it at that. I was told PEMDAS and did PEMDAS.
Uh… no the 1 is wrong? Division and multiplication have the same precedence, so the correct order is to evaluate from left to right, resulting in 16.
The real correct order is to use brackets to remove ambiguity.
Exactly, these types of problems are designed to make people confused and discuss PEMDAS and drive social media engagement.
For anyone like me who has math as their worst subject
Admits they suck at math.
Tries to correct the math.
Is wrong.
I’m fuckin’ dead rn 💀
Me searching the place for my old Ti83 after stumbling on this thread.
My partner: why are you even looking for this thing??
Me: Somebody on the Internet is WRONG.
My partner: Good enough, I’ll help!
You’re a lifesaver, thank you so much. I actually didn’t know about PEMDAS, I was never taught it before…
They’re actually wrong though.
There’s 4 levels to PEMDAS, not 6.
- Parenthese
- Exponent
- Multiplication or Division
- Addition or Substraction
Also,
https://www.symbolab.com/solver/step-by-step/8\div2(2%2B2)?or=input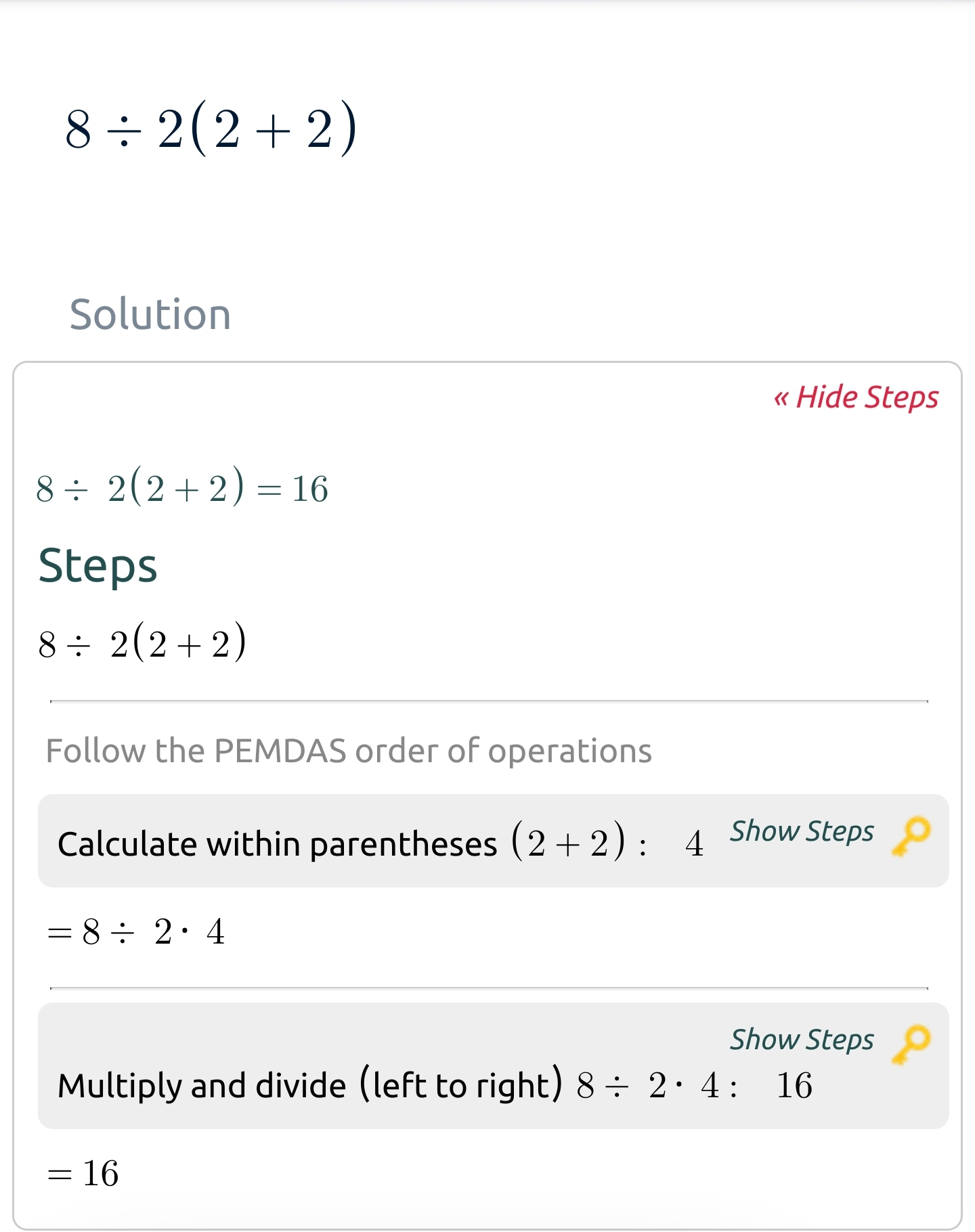
Like @LopensLeftArm@sh.itjust.works mentioned:
PEMDAS should be read as Parentheses, Exponents, Multiplication and Division, Addition and Subtraction. There are four levels of priority, not six.
- Read the Parentheses of
pink tax strikes again
8÷2(2+2)=2(2+2)÷2(2+2)
alternatively if 8÷2(2+2)=16 that means 2(2+2)=8÷16 in other words 8=0,5 which it isnt
your first line is correct, but while it looks like 1 (and it might be under different conventions), evaluating according to standard rules (left to right if not disambiguated by pemdas) yields
2(2+2)/2(2+2) = 2(4)/2(4) = 2*4/2*4 = 8/2*4 = 4*4 = 16
Using implicit multiplication in quotients is weird and really shouldn’t happen, this would usually be written as 8/(2*(2+2)) or 8/2*(2+2) and both are much clearer
Your second argument only works if you treat 2(2+2) as a single “thing”, which it looks like, but isn’t, in this case
not much to refute in the argument of whether its 16 or 1 as its all a matter of convention in the end and ultimately the root of the argument is poor formatting of the expression, im used to implicit multiplication taking precedent and that 2(2+2)===2*(2+2) and that for my first argument having the same expression on 2 sides of a division sign automatically equals 1, but how come you find implicit multiplication in quotients weird? seeing as it happens literally all the time in equations, unless thats a difference in school systems or similar im unaware of
for fun also rewrote the expression into powers of 2 and indeed depending on how you go about implicit multiplication i end up with either 2⁰ or 2⁴, so for the sake of sanity i figure its best to just say x₁=1; x₂=16
It’s weird because usually the people writing the expressions want to communicate clearly, and stuff like 1/2x is not immediately clear to everyone, so they write the 1/2 as a fraction.
The same expression on both sides of the division sign only reduce to one if they actually bind to the division sign, which is rarely an issue, but that is exactly the thing that is in question here. I think it’s clear that 1 + 1/1 + 1 is 3, not 1, even though 1+1 = 1+1.
But as you said, of course, the evaluation order is just convention, you can just as well write everything in https://en.m.wikipedia.org/wiki/Reverse_Polish_notation
this comment section illustrates perfectly why i hate maths so much lmao
love ambiguous, confusing rules nobody can even agree on!
The problem isn’t math, it’s the people that suck at at it who write ambigous terms like this, and all the people in the comments who weren’t educated properly on what conventions are.
Yeah, you could easily make this more straightforward by putting parentheses around 8÷2. It’s like saying literature sucks because Finnegans Wake is incomprehensible.
lol, math is literally the only subject that has rules set in stone. This example is specifically made to cause confusion. Division has the same priority as multiplication. You go from left to right. problem here is the fact that you see divison in fraction form way more commonly. A fraction could be writen up as (x)/(y) not x/y (assuming x and y are multiple steps). Plain and simple.
The fact that some calculator get it wrong means that the calculator is wrongly configured. The fact that some people argue that you do () first and then do what’s outside it means that said people are dumb.
They managed to get me once too, by everyone spreading missinformation so confidently. Don’t even trust me, look up the facts for yourself. And realise that your comment is just as incorrect as everyone who said the answer is 1. (uhm well they don’t agree on 0^0, but that’s kind of a paradox)
Off topic, but the rules of math are not set in stone. We didn’t start with ZFC, some people reject the C entirely, then there is intuitionistic logic which I used to laugh at until I learned about proof assistants and type theory. And then there are people who claim we should treat the natural numbers as a finite set, because things we can’t compute don’t matter anyways.
On topic: Parsing notation is not a math problem and if your notation is ambiguous or unclear to your audience try to fix it.
math is literally the only subject that has rules set in stone
go past past high school and this isn’t remotely true
there are areas of study where 1+1=1
In modular arithmetic you can make 1+1=0 but I’m struggling to think of a situation where 1+1=1 without redefining the + and = functions.
Not saying you’re wrong, but do you have an example? I’d be interested to see
If we had 1/2x, would you interpret that as 0.5x, or 1/(2x)?
Because I can guarantee you almost any mathematician or physicist would assume the latter. But the argument you’re making here is that it should be 0.5x.
It’s called implicit multiplication or “multiplication indicated by juxtaposition”, and it binds more tightly than explicit multiplication or division. The American Mathematical Society and American Physical Society both agree on this.
BIDMAS, or rather the idea that BIDMAS is the be-all end-all of order of operations, is what’s known as a “lie-to-children”. It’s an oversimplification that’s useful at a certain level of understanding, but becomes wrong as you get more advanced. It’s like how your year 5 teacher might have said “you can’t take the square root of a negative number”.
An actual mathematician or physicist would probably ask you to clarify because they don’t typically write division inline like that.
That said, Wolfram-Alpha interprets “1/2x” as 0.5x. But if you want to argue that Wolfram-Alpha’s equation parser is wrong go ahead.
I will happily point out that Wolfram Alpha does this wrong. So do TI calculators, but not Casio or Sharp.
Go to any mathematics professor and give them a problem that includes 1/2x and ask them to solve it. Don’t make it clear that merely asking “how do you parse 1/2x?” is your intent, because in all likelihood they’ll just tell you it’s ambiguous and be done with it. But if it’s written as part of a problem and they don’t notice your true intent, you can guarantee they will take it as 1/(2x).
Famed physicist Richard Feynman uses this convention in his work.
In fact, even around the time that BIDMAS was being standardised, the writing being done doing that standardisation would frequently use juxtaposition at a higher priority than division, without ever actually telling the reader that’s what they were doing. It indicates that at the time, they perhaps thought it so obvious that juxtaposition should be performed first that it didn’t even need to be explained (or didn’t even occur to them that they could explain it).
According to Casio, they do juxtaposition first because that’s what most teachers around the world want. There was a period where their calculators didn’t do juxtaposition first, something they changed to because North American teachers were telling them they should, but the outcry front the rest of the world was enough for them to change it back. And regardless of what teachers are doing, even in America, professors of mathematics are doing juxtaposition first.
I think this problem may ultimately stem from the very strict rote learning approach used by the American education system, where developing a deeper understanding of what’s going on seems to be discouraged in favour of memorising facts like “BIDMAS”.
To be clear, I’m not saying 1/2x being 1/(2x) rather than 0.5x is wrong. But it’s not right either. I’m just pretty firmly in the “inline formulae are ambiguous” camp. Whichever rule you pick, try to apply it consistently, but use some other notation or parenthesis when you want to be clearly understood.
The very fact that this conversation even happens is proof enough that the ambiguity exists. You can be prescriptive about which rules are the correct ones all you like, but that’s not going to stop people from misunderstanding. If your goal is to communicate clearly, then you use a more explicit notation.
Even Wolfram Alpha makes a point of restating your input to show how it’s being interpreted, and renders “1/2x” as something more like
1 - x 2to make very clear what it’s doing.
Even Wolfram Alpha makes a point of restating your input to show how it’s being interpreted
This is definitely the best thing to do. It’s what Casio calculators do, according to those videos I linked.
My main point is that even though there is theoretically an ambiguity there, the way it would be interpreted in the real world, by mathematicians working by hand (when presented in a way that people aren’t specifically on the lookout for a “trick”) would be overwhelmingly in favour of juxtaposition being evaluated before division. Maybe I’m wrong, but the examples given in those videos certainly seem to point towards the idea that people performing maths at a high level don’t even think twice about it.
And while there is a theoretical ambiguity, I think any tool which is operating counter to how actual mathematicians would interpret a problem is doing the wrong thing. Sort of like a dictionary which decides to take an opinionated stance and say “people are using the word wrong, so we won’t include that definition”. Linguists would tell you the job of a dictionary should be to describe how the word is used, not rigidly stick to some theoretical ideal. I think calculators and tools like Wolfram Alpha should do the same with maths.
Linguists would tell you the job of a dictionary should be to describe how the word is used, not rigidly stick to some theoretical ideal. I think calculators and tools like Wolfram Alpha should do the same with maths.
You’re literally arguing that what you consider the ideal should be rigidly adhered to, though.
“How mathematicians do it is correct” is a fine enough sentiment, but conveniently ignores that mathematicians do, in fact, work at WolframAlpha, and many other places that likely do it “wrong”.
The examples in the video showing inline formulae that use implicit priority have two things in common that make their usage unambiguous.
First, they all are either restating, or are derived from, formulae earlier in the page that are notated unambiguously, meaning that in context there is a single correct interpretation of any ambiguity.Second, being a published paper it has to adhere to the style guide of whatever body its published under, and as pointed out in that video, the American Mathematical Society’s style guide specifies implicit priority, making it unambiguous in any of their published works. The author’s preference is irrelevant.
Also, if it’s universally correct and there was no ambiguity in its use among mathematicians, why specify it in the style guide at all?
PEMDAS
Parenthesis, exponents, multiplication, division, addition, subtraction.
The rule is much older than me and they taught it in school. Nothing ambiguous about it, homie. The phone app is fucked up. Calculator nailed it.
i know about pemdas and also my brother in christ half the people in the comments are saying the phone app is right lmao
edit: my first answer was 16
The comment from subignition explains that the phone’s answer, 16, is what you get by strictly following PEMDAS: the rule is that multiplication and division have the same precedence, and you evaluate them from left-to-right.
The calculator uses a different convention where either multiplication has higher priority than division, or where “implicit” multiplication has higher priority (where there is no multiply sign between adjacent expressions).
But explicit multiplication is part of the parenthesis, so still comes before division or exponent
The parentheses step only covers expressions inside parentheses. That’s 2 + 2 in this case. The times-2 part is outside the parentheses so it’s evaluated in a different step.



















